Page 8 - Ragonese_Bianchini_1996

132 S. Ragonese, M.L. Bianchini l Fisheries Research 26 ( 1996) 125-137

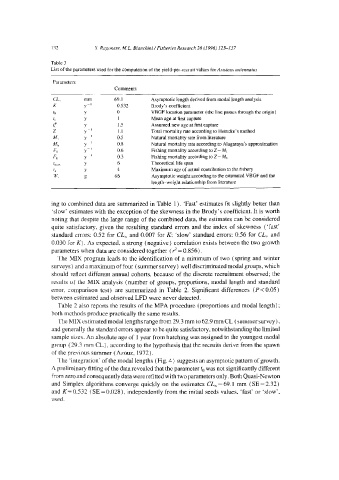
T ab le 3
List of the parameters used for the computation of the yield-per-recruit values for Aristeus anrennatus

Parameters
Comments
CL m m 69.1 Asymptotic length derived from modallength analysis
K y-1 0.532 Brody' s coeffìcient
lo y o VBGF location parameter ( the li ne passes through the ori gin)
t, y Mean age at fìrst capture
t, * y 1.5 Assumed new age at fìrst capture
z y- l 1.1 Total mortality rate according t o Heincke' s method
M, y- l 0.5 Natura! mortality rate from literature
M" y- l 0.8 Natura! mortality rate according to Alagaraya's approximation
y-1
F l 0.6 Fishing mortality according to Z- M,
F, y-1 0.3 Fishing mortality according to Z- M"
y 6 Theoretical !ife span
flll<IX
t, y 4 Maximum age of actual contribution to the fishery
W. g 66 Asymptotic weight according to the estimated VBGF and the
length-weight relationship from literature

ing to combined data are summarized in Table l). 'Fast' estimates fit slightly better than
'slow' estimates with the exception of the skewness in the Brody's coefficient. It is worth
noting that despite the large range of the combined data, the estimates can be considered
qui te satisfactory, given the resulting standard errors and the in de x of skewness ('fast'
standard errors: 0.52 for CLx and 0.007 for K; 'slow' standard errors: 0.56 for CL.c and
0.030 for K). As expected, a strong (negative) correlation exists between the two growth
parameters when data are considered together (? = 0.856).
The MIX program leads to the identification of a minimum of two ( spring and winter
surveys) an d a maximum of four ( summer survey) well discriminated moda! groups, which
should reftect different annua! cohorts, because of the discrete recruitment observed; the
rcsults of the MIX analysis ( number of groups, proportions, moda! length and standard
error, comparison test) are summarized in Table 2. Significant differences (P< 0.05)
between estimated and observed LFD were never detected.
Table 2 al so reports the results of the MPA procedure ( proportions an d modallength);
both methods produce practically the same results.
The MIX estimated modallengths range from 29.3 m m to 62.9 mm CL ( summer survey),
and generally the standard errors appear to be qui te satisfactory, notwithstanding the limited
sample sizes. An absolute age of l year from hatching was assigned to the youngest moda!
group (29.3 mm CL), according to the hypothesis that the recruits derive from the spawn
of the previous summer ( Azouz, 1972).
The 'integration' of the modallengths (Fig. 4) suggests an asymptotic pattern of growth.
A preliminary fitting of the data revealed that the parameter t 0 was not significantly different
from zero an d consequently data w ere refitted with two parameters only. Both Quasi-Newton
and Simplex algorithms converge quickly on the estimates CLx = 69.1 mm (SE= 2.32)
and K=0.532 (SE=0.028), independently from the initial seeds values, 'fast' or 'slow',
used.