Page 8 - Rouyer_Fromentin_2008

18 Mar Ecol Prog Ser 359: 11–23, 2008

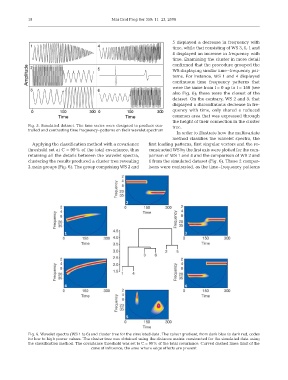
5 displayed a decrease in frequency with
time, while that consisting of WS 3, 6, 1 and
4 displayed an increase in frequency with
time. Examining the cluster in more detail
confirmed that the procedure grouped the
WS displaying similar time–frequency pat-
terns. For instance, WS 1 and 4 displayed
continuous time–frequency patterns that
were the same from t = 0 up to t = 150 (see
also Fig. 6); these were the closest of the
dataset. On the contrary, WS 2 and 5, that
displayed a discontinuous decrease in fre-
quency with time, only shared a reduced
common area that was expressed through
the height of their connection in the cluster
Fig. 5. Simulated dataset. The time series were designed to produce con- tree.
trolled and contrasting time frequency–patterns on their wavelet spectrum
In order to illustrate how the multivariate
method classifies the wavelet spectra, the
Applying the classification method with a covariance first leading patterns, first singular vectors and the re-
threshold set at C = 99% of the total covariance, thus constructed WS by the first axis were plotted for the com-
retaining all the details between the wavelet spectra, parison of WS 1 and 4 and the comparison of WS 2 and
clustering the results produced a cluster tree revealing 6 from the simulated dataset (Fig. 6). These 2 compar-
2 main groups (Fig. 6). The group comprising WS 2 and isons were contrasted, as the time–frequency patterns

Fig. 6. Wavelet spectra (WS 1 to 6) and cluster tree for the simulated data. The colour gradient, from dark blue to dark red, codes
for low to high power values. The cluster tree was obtained using the distance matrix constructed for the simulated data using
the classification method. The covariance threshold was set to C = 99% of the total covariance. Curved dashed lines: limit of the
cone of influence, the area where edge effects are present